Bayes v. Frequentist — Bayes’s Billiards (continued)

Introduction | Coin Problem | Bayes’s Rule: History | Bayes’s Rule: Derivation | Billiards Problem | Billiards (continued) | Endnotes | References

Billiards Problem (continued)

I like to think of the balls that Bayes imagines throwing as pool balls with ball \(W\) as the (white) cue ball, and ball \(O\) as the (orange) 5-ball.

So, here is the billiards problem:

A cue ball \(W\)is tossed from the right end onto a billiards table and ends up at an unknown distance \(\theta\) from the right. Then an (orange) 5-ball \(O\) is tossed and ends up nearer to the right end than the cue ball \(W\). This is arbitrarily called a “success”. Given this one success, what is the probability that the cue ball \(W\) made it more than halfway across the table? In other words what is \(P(0.5 < \theta <1)\)?

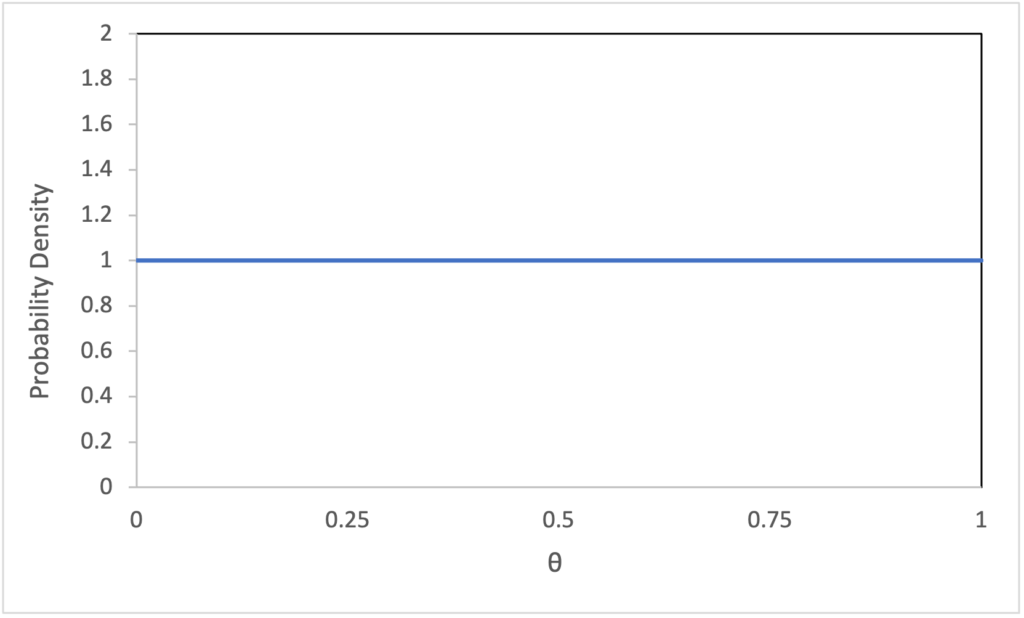
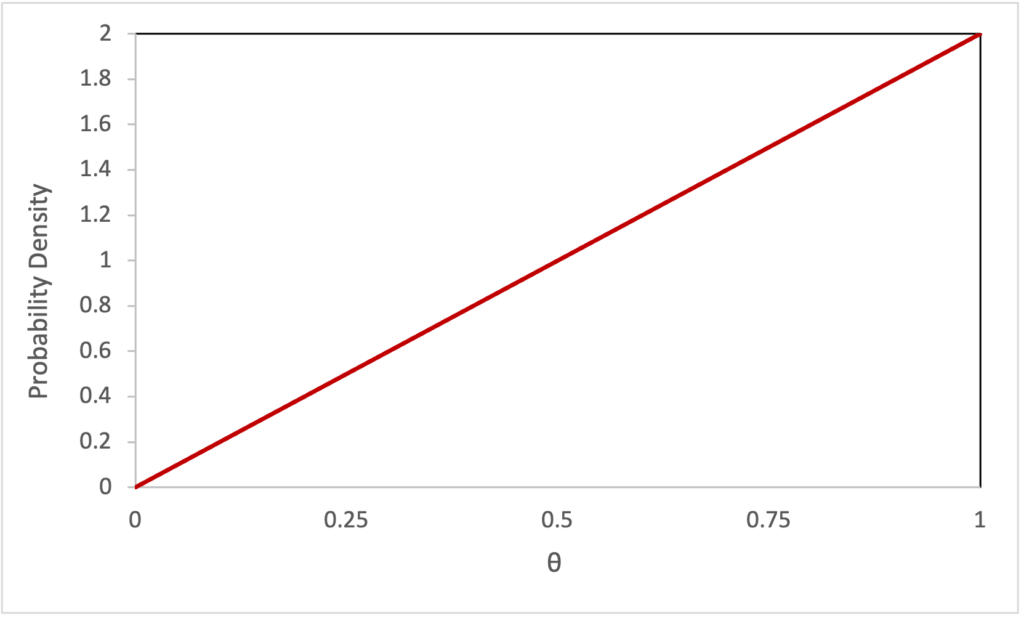
Again, the billiards problem is more difficult than the coin problem. We have moved from a discrete uniform probability distribution \(P(\theta)\) to a continuous uniform probability density function \(p(\theta)\). I will use upper case \(P(\theta)\) for the discrete probability distribution, also called the probability mass function (PMF), and I will use lower case \(p(\theta)\) for the continuous probability density function (PDF). If you are new to PDFs, they take some getting used to. Like a probability, a probability density is always greater than or equal to 0, \(p(\theta) \geq 0\), but it doesn’t have to be less than 1. In a figure, probability is no longer represented by the height of a discrete point but by the area under the continuous PDF (\(P(\theta_a < \theta < \theta_b) = \int_{\theta_a}^{\theta_b} p(\theta) d\theta\)). For the PDF to be valid, the area under it over the entire range of \(\theta\) must equal 1 (\(\int_{-\infty}^{+\infty} p(\theta) d\theta = 1\)).

This is the uniform probability density function (PDF) for the variable \(\theta\) prior to any trials. The probability that \(\theta\) is between any two values is the area under the PDF between those two values.

This is the posterior probability density function (PDF) for the variable \(\theta\) after seeing one success. The probability that \(\theta\) is between any two values is the area under the PDF between those two values. The area under the curve from \(\theta = 0.5\) to \(\theta = 1\) is \(\frac{3}{4}\).

The remainder of this article is available in the pdf. Link to the pdf.

(next) Endnotes

Introduction | Introduction | Coin Problem | Bayes’s Rule: History | Bayes’s Rule: Derivation | Billiards Problem | Billiards (continued) | Endnotes | References