© 26 January 2023 by Michael A. Kohn
Link to the pdf if this article
Introduction | Coin Problem | Bayes’s Rule: History | Bayes’s Rule: Derivation | Billiards Problem | Billiards (continued) | Endnotes | References
Billiards Problem
The billiards problem is the focus of Bayes’s essay, but it is harder than the coin problem. Both problems start with the probability of “success” in a binary trial. In the coin problem, we designate heads as a “success”, and there are three discrete success probabilities: 0.0 for the 2-tailed coin; 0.5 for the fair coin; and 1.0 for the 2-headed coin. As we shall see, in the billiards problem, the success probability ranges continuously from 0 to 1. To move from the coin problem to the billiards problem, I introduce a variable \( \theta \) equal to the probability of success on a single trial. For the 2-tailed coin, \( \theta = 0\); for the fair coin, \( \theta =0.5\), and for the 2-headed coin, \( \theta = 1 \). Since the probability of selecting each of the three coins is \( \frac{1}{3} \), before the coin toss,
\begin{align*} P(\theta \! = \! 0) &= \frac{1}{3} \quad \text{(2-tailed)}\\ P(\theta \! = \! 0.5) &= \frac{1}{3} \quad \text{(fair)}\\ P(\theta \! = \! 1) &= \frac{1}{3} \quad \text{(2-headed)} \end{align*}This can be confusing because \(\theta\) is itself a probability which can take on three possible values, so \(\frac{1}{3}\) is the probability of a probability.
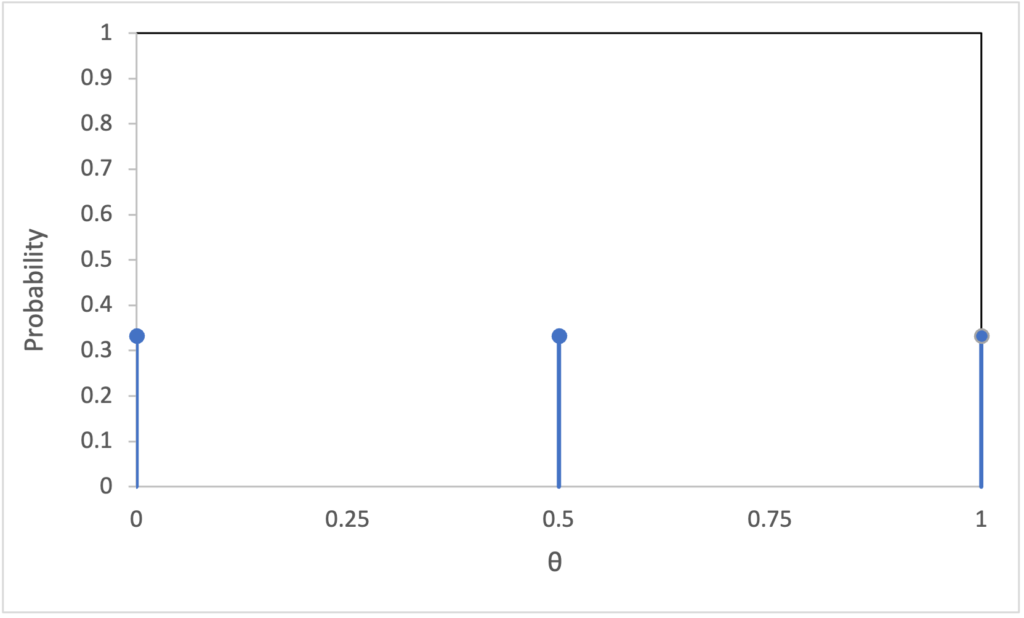
What is the distribution of \( \theta \) after the coin has come up heads on a single toss? We already know that, after seeing heads, the probability of the 2-headed coin (\( \theta = 1\)) is \(\frac{2}{3}\). The possibility of a 2-tailed coin has been eliminated, so \(P(\theta=0.0)=0\). That leaves only the fair coin, so \(P(\theta = 0.5) = \frac{1}{3}\).

In the billiards problem, the success probability \( \theta \) isn’t limited to being 0, 0.5, or 1. Bayes assumes that \(\theta\) is equally likely to take on any value between 0 and 1. It’s easy to imagine selecting \(\theta\) from three equally likely alternatives, but how does one imagine selecting \( \theta \) from any of the possible values between 0 and 1? Bayes describes a hypothetical square table onto which someone else (besides Bayes) throws a ball labelled \( W \) from the right end. I follow many others and call the table a billiard table although Bayes never mentions billiards. Picture Bayes sitting with his back to the table because he doesn’t know where ball \(W\) ends up, but it is equally likely to end up anywhere along the length of the table. To get \(\theta\) (which is unknown to Bayes), divide the distance of \(W\) from the right side of the table by the length of the table.
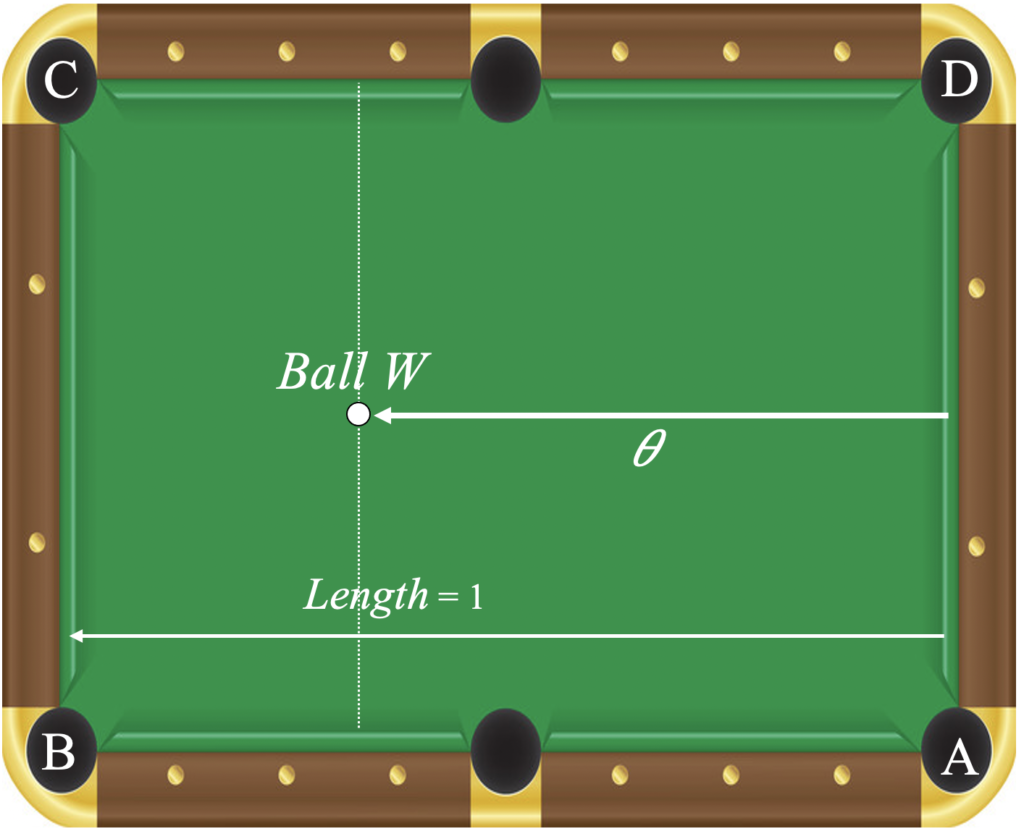
Bayes’s binary event is not tossing a coin for heads or tails. Instead, while he still has his back to the table, the same “someone else” tosses a second ball \(O\) onto it. The equivalent of “heads” is having \(O\) end up to the right of the first ball \(W\). We will call this a “success”. After tossing ball \(O\), the “someone else” reports the result, success or failure. Ball \(O\) can be tossed repeatedly, but we will start with one round. Based on the result, Bayes calculates the probability that \( \theta \) is in a particular range, say between 0.5 and 1, which is the probability that the first ball \(W \) made it more than halfway across the table.